Ghost Code¶
What is ghost code?¶
ghost code is part of the program that is added for the purpose of specification
Why3 team, “The Spirit of Ghost Code”
... or verification
addition by SPARK team
Examples of ghost code:
contracts (
Pre,Post,Contract_Cases, etc.)assertions (
pragma Assert, loop (in)variants, etc.)special values
Func'Result,Var'Old,Var'Loop_Entry
Is it enough?
Ghost code – A trivial example¶
how to express it?
package Show_Trivial_Example is
type Data_Array is array (1 .. 10) of Integer;
Data : Data_Array;
Free : Natural;
procedure Alloc;
end Show_Trivial_Example;
package body Show_Trivial_Example is
procedure Alloc is
begin
-- some computations here
--
-- assert that Free “increases”
null;
end Alloc;
end Show_Trivial_Example;
Ghost variables – aka auxiliary variables¶
Variables declared with aspect
Ghostdeclaration is discarded by compiler when ghost code ignored
Ghost assignments to ghost variables
assignment is discarded by compiler when ghost code ignored
package Show_Ghost_Variable is
type Data_Array is array (1 .. 10) of Integer;
Data : Data_Array;
Free : Natural;
procedure Alloc;
end Show_Ghost_Variable;
package body Show_Ghost_Variable is
procedure Alloc is
Free_Init : Natural with Ghost;
begin
Free_Init := Free;
-- some computations here
pragma Assert (Free > Free_Init);
end Alloc;
end Show_Ghost_Variable;
Ghost variables – non-interference rules¶
Ghost variable cannot be assigned to non-ghost one
Free := Free_Init;
Ghost variable cannot indirectly influence assignment to non-ghost one
if Free_Init < Max then
Free := Free + 1;
end if;
procedure Show_Non_Interference is
type Data_Array is array (1 .. 10) of Integer;
Data : Data_Array;
Free : Natural;
Free_Init : Natural with Ghost;
procedure Alloc is
begin
Free_Init := Free;
-- some computations here
pragma Assert (Free > Free_Init);
end Alloc;
procedure Assign (From : Natural; To : out Natural) is
begin
To := From;
end Assign;
begin
Assign (From => Free_Init, To => Free);
end Show_Non_Interference;
Ghost statements¶
Ghost variables can only appear in ghost statements
assignments to ghost variables
assertions and contracts
calls to ghost procedures
procedure Show_Ghost_Statements is
type Data_Array is array (1 .. 10) of Integer;
Data : Data_Array;
Free : Natural;
Free_Init : Natural with Ghost;
procedure Alloc is
begin
Free_Init := Free;
-- some computations here
pragma Assert (Free > Free_Init);
end Alloc;
procedure Assign (From : Natural; To : out Natural)
with Ghost
is
begin
To := From;
end Assign;
begin
Assign (From => Free, To => Free_Init);
end Show_Ghost_Statements;
procedure Show_Ghost_Statements is
begin
-- Non-ghost variable "Free" cannot appear as actual in
-- call to ghost procedure
Assign (From => Free_Init, To => Free);
end Show_Ghost_Statements;
Ghost procedures¶
Ghost procedures cannot write into non-ghost variables
procedure Assign (Value : Natural) with Ghost is
begin
-- "Free" is a non-ghost variable
Free := Value;
end Assign;
Used to group statements on ghost variables
in particular statements not allowed in non-ghost procedures
procedure Assign_Cond (Value : Natural) with Ghost is
begin
if Condition then
Free_Init := Value;
end if;
end Assign_Cond;
Can have
Global(includingProof_In) &Dependscontracts
Ghost functions¶
Functions for queries used only in contracts
Typically implemented as expression functions
in private part – proof of client code can use expression
or in body – only proof of unit can use expression
package Show_Ghost_Function is
type Data_Array is array (1 .. 10) of Integer;
Data : Data_Array;
Free : Natural;
Free_Init : Natural with Ghost;
procedure Alloc with
Pre => Free_Memory > 0,
Post => Free_Memory < Free_Memory'Old;
function Free_Memory return Natural with Ghost;
private
-- Completion of ghost function declaration
function Free_Memory return Natural is
(0); -- dummy implementation
-- If function body as declaration:
--
-- function Free_Memory return Natural is (...) with Ghost;
end Show_Ghost_Function;
Imported ghost functions¶
Ghost functions without a body
cannot be executed
function Free_Memory return Natural with Ghost, Import;
Typically used with abstract ghost private types
definition in
SPARK_Mode(Off)type is abstract for GNATprove
package Show_Imported_Ghost_Function
with SPARK_Mode => On is
type Memory_Chunks is private;
function Free_Memory return Natural with Ghost;
function Free_Memory return Memory_Chunks
with Ghost, Import;
private
pragma SPARK_Mode (Off);
type Memory_Chunks is null record;
end Show_Imported_Ghost_Function;
Definition of ghost types/functions given in proof
either in Why3 using
External_Axiomatizationor in an interactive prover (Coq, Isabelle, etc.)
Ghost packages and ghost abstract state¶
Every entity in a ghost package is ghost
local ghost package can group all ghost entities
library-level ghost package can be withed/used in regular units
Ghost abstract state can only represent ghost variables
package Show_Ghost_Package
with Abstract_State => (State with Ghost) is
function Free_Memory return Natural with Ghost;
end Show_Ghost_Package;
package body Show_Ghost_Package
with Refined_State => (State => (Data, Free, Free_Init)) is
type Data_Array is array (1 .. 10) of Integer;
Data : Data_Array with Ghost;
Free : Natural with Ghost;
Free_Init : Natural with Ghost;
function Free_Memory return Natural is
(0); -- dummy implementation
end Show_Ghost_Package;
Non-ghost abstract state can contain both ghost and non-ghost variables
Executing ghost code¶
Ghost code can be enabled globally
using compilation switch
-gnata(for all assertions)
Ghost code can be enabled selectively
using
pragma Assertion_Policy (Ghost => Check)SPARK rules enforce consistency – in particular no write disabled
package Show_Exec_Ghost_Code is
pragma Assertion_Policy (Ghost => Check);
-- pragma Assertion_Policy (Ghost => Ignore, Pre => Check);
procedure Alloc with
Pre => Free_Memory > 0;
function Free_Memory return Natural with Ghost;
end Show_Exec_Ghost_Code;
GNATprove analyzes all ghost code and assertions
Examples of use¶
Encoding a state automaton¶
Tetris in SPARK
at Tetris
Global state encoded in global ghost variable
updated at the end of procedures of the API
type State is (Piece_Falling, ...) with Ghost;
Cur_State : State with Ghost;
Properties encoded in ghost functions
function Valid_Configuration return Boolean is
(case Cur_State is
when Piece_Falling => ...,
when ...)
with Ghost;
Expressing useful lemmas¶
GCD in SPARK
at GCD
Lemmas expressed as ghost procedures
procedure Lemma_Not_Divisor (Arg1, Arg2 : Positive) with
Ghost,
Global => null,
Pre => Arg1 in Arg2 / 2 + 1 .. Arg2 - 1,
Post => not Divides (Arg1, Arg2);
Most complex lemmas further refined into other lemmas
code in procedure body used to guide proof (e.g. for induction)
Specifying an API through a model¶
Red black trees in SPARK
Invariants of data structures expressed as ghost functions
using
Type_Invarianton private types
Model of data structures expressed as ghost functions
called from
Pre/Postof subprograms from the API
Lemmas expressed as ghost procedures
sometimes without contracts to benefit from inlining in proof
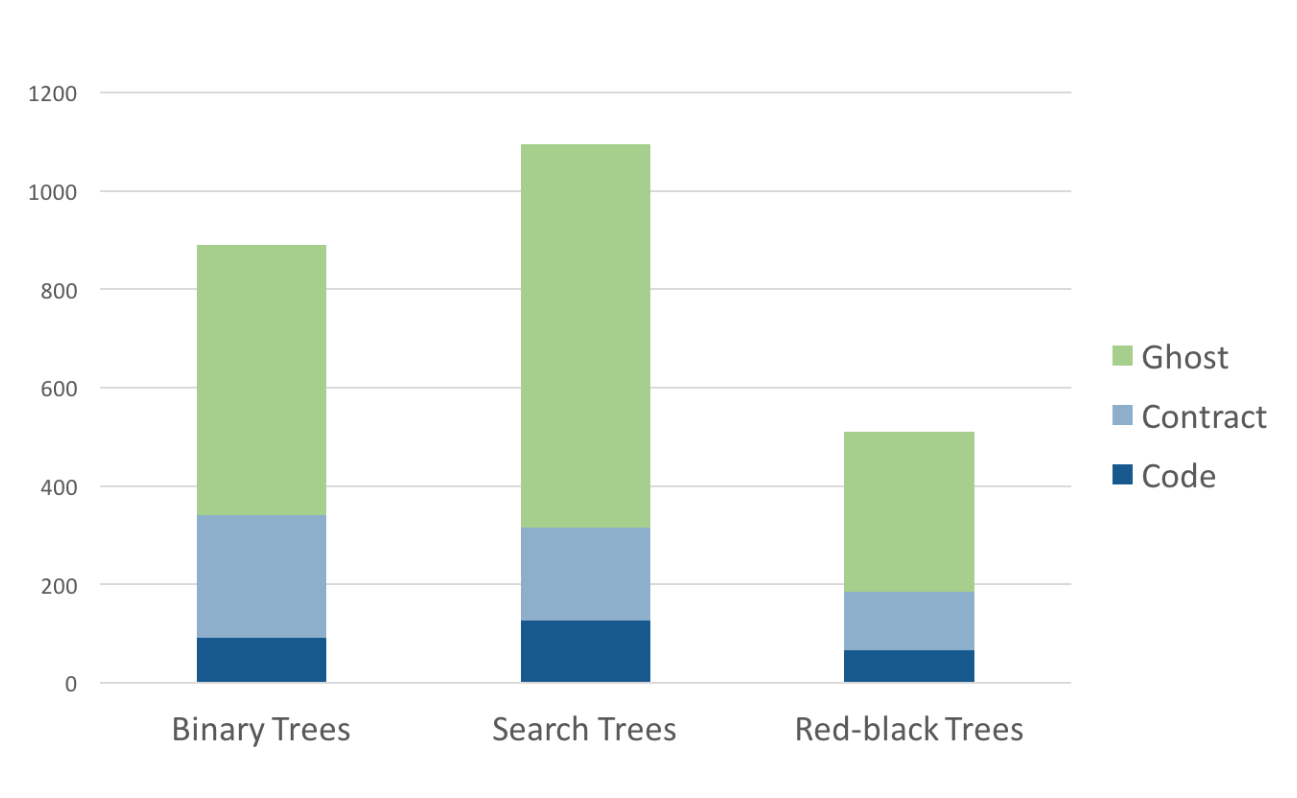
Extreme proving with ghost code – red black trees in SPARK¶
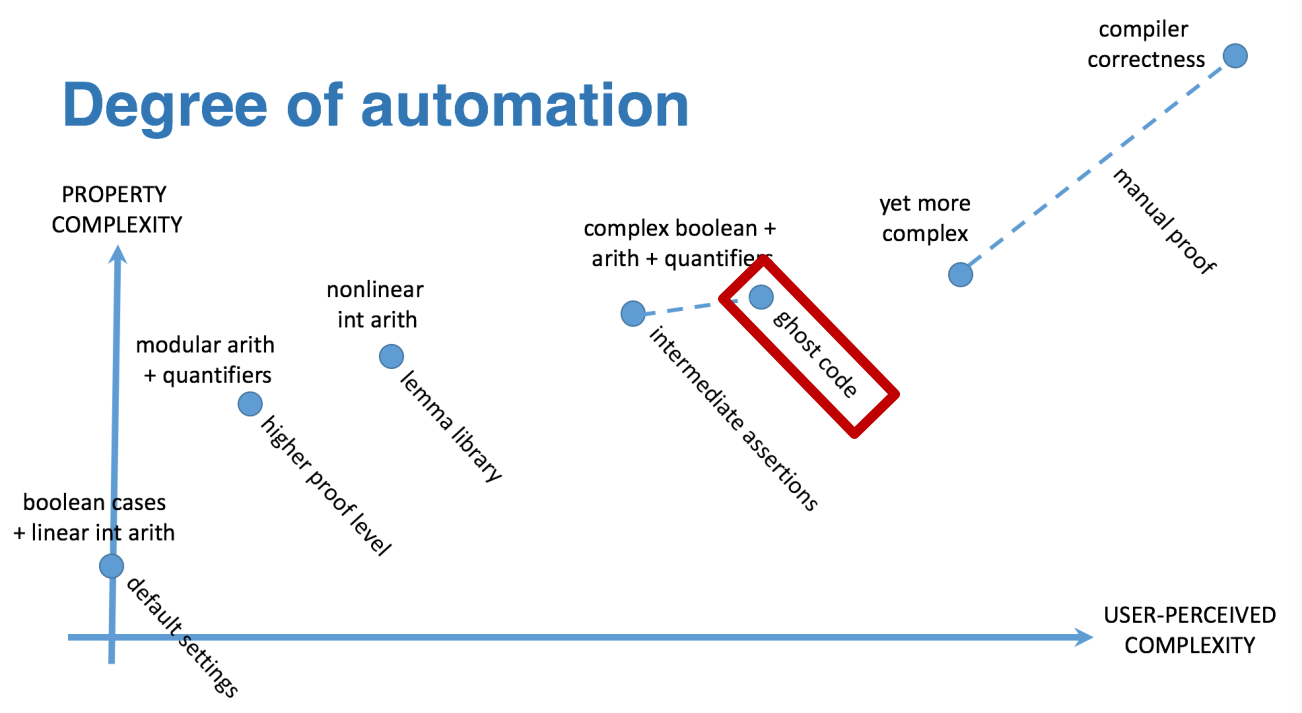
Positioning ghost code in proof techniques¶
Code Examples / Pitfalls¶
Example #1¶
procedure Example_01 is
type Data_Array is array (1 .. 10) of Integer;
Data : Data_Array;
Free : Natural;
procedure Alloc is
Free_Init : Natural with Ghost;
begin
Free_Init := Free;
-- some computations here
if Free <= Free_Init then
raise Program_Error;
end if;
end Alloc;
begin
null;
end Example_01;
This code is not correct. A ghost entity cannot appear in this context.
Example #2¶
procedure Example_02 is
type Data_Array is array (1 .. 10) of Integer;
Data : Data_Array;
Free : Natural;
procedure Alloc is
Free_Init : Natural with Ghost;
procedure Check with Ghost is
begin
if Free <= Free_Init then
raise Program_Error;
end if;
end Check;
begin
Free_Init := Free;
-- some computations here
Check;
end Alloc;
begin
null;
end Example_02;
This code is correct. Note that procedure Check is inlined for proof
(no contract).
Example #3¶
package Example_03 is
type Data_Array is array (1 .. 10) of Integer;
Data : Data_Array;
Free : Natural;
pragma Assertion_Policy (Pre => Check);
procedure Alloc with
Pre => Free_Memory > 0;
function Free_Memory return Natural with Ghost;
end Example_03;
This code is not correct. Incompatible ghost policies in effect during compilation, as ghost code is ignored by default. Note that GNATprove accepts this code as it enables all ghost code and assertions.
Example #4¶
package Example_04 is
procedure Alloc with
Post => Free_Memory < Free_Memory'Old;
function Free_Memory return Natural with Ghost;
end Example_04;
package body Example_04 is
Free : Natural;
Max : constant := 1000;
function Free_Memory return Natural is
begin
return Max - Free + 1;
end Free_Memory;
procedure Alloc is
begin
Free := Free + 10;
end Alloc;
end Example_04;
This code is not correct. No postcondition on Free_Memory that would
allow proving the postcondition on Alloc.
Example #5¶
package Example_05 is
procedure Alloc with
Post => Free_Memory < Free_Memory'Old;
function Free_Memory return Natural with Ghost;
end Example_05;
package body Example_05 is
Free : Natural;
Max : constant := 1000;
function Free_Memory return Natural is (Max - Free + 1);
procedure Alloc is
begin
Free := Free + 10;
end Alloc;
end Example_05;
This code is correct. Free_Memory has an implicit postcondition as an
expression function.
Example #6¶
procedure Example_06 is
subtype Resource is Natural range 0 .. 1000;
subtype Num is Natural range 0 .. 6;
subtype Index is Num range 1 .. 6;
type Data is array (Index) of Resource;
function Sum (D : Data; To : Num) return Natural is
(if To = 0 then 0 else D (To) + Sum (D, To - 1))
with Ghost;
procedure Create (D : out Data) with
Post => Sum (D, D'Last) < 42
is
begin
for J in D'Range loop
D (J) := J;
pragma Loop_Invariant (2 * Sum (D, J) <= J * (J + 1));
end loop;
end Create;
begin
null;
end Example_06;
This code is not correct. Info: expression function body not available for
proof (Sum may not return).
Example #7¶
procedure Example_07 is
subtype Resource is Natural range 0 .. 1000;
subtype Num is Natural range 0 .. 6;
subtype Index is Num range 1 .. 6;
type Data is array (Index) of Resource;
function Sum (D : Data; To : Num) return Natural is
(if To = 0 then 0 else D (To) + Sum (D, To - 1))
with Ghost, Annotate => (GNATprove, Terminating);
procedure Create (D : out Data) with
Post => Sum (D, D'Last) < 42
is
begin
for J in D'Range loop
D (J) := J;
pragma Loop_Invariant (2 * Sum (D, J) <= J * (J + 1));
end loop;
end Create;
begin
null;
end Example_07;
This code is correct. Note that GNATprove does not prove the termination
of Sum here.
Example #8¶
procedure Example_08 is
subtype Resource is Natural range 0 .. 1000;
subtype Num is Natural range 0 .. 6;
subtype Index is Num range 1 .. 6;
type Data is array (Index) of Resource;
function Sum (D : Data; To : Num) return Natural is
(if To = 0 then 0 else D (To) + Sum (D, To - 1))
with Ghost, Annotate => (GNATprove, Terminating);
procedure Create (D : out Data) with
Post => Sum (D, D'Last) < 42
is
begin
for J in D'Range loop
D (J) := J;
end loop;
end Create;
begin
null;
end Example_08;
This code is correct. The loop is unrolled by GNATprove here, as
D'Range is 0 .. 6. The automatic prover unrolls the
recursive definition of Sum.
Example #9¶
with Ada.Containers.Functional_Vectors;
procedure Example_09 is
subtype Resource is Natural range 0 .. 1000;
subtype Index is Natural range 1 .. 42;
package Seqs is new
Ada.Containers.Functional_Vectors (Index, Resource);
use Seqs;
function Create return Sequence with
Post => (for all K in 1 .. Last (Create'Result) =>
Get (Create'Result, K) = K)
is
S : Sequence;
begin
for K in 1 .. 42 loop
S := Add (S, K);
end loop;
return S;
end Create;
begin
null;
end Example_09;
This code is not correct. Loop requires a loop invariant to prove the postcondition.
Example #10¶
with Ada.Containers.Functional_Vectors;
procedure Example_10 is
subtype Resource is Natural range 0 .. 1000;
subtype Index is Natural range 1 .. 42;
package Seqs is new
Ada.Containers.Functional_Vectors (Index, Resource);
use Seqs;
function Create return Sequence with
Post => (for all K in 1 .. Last (Create'Result) =>
Get (Create'Result, K) = K)
is
S : Sequence;
begin
for K in 1 .. 42 loop
S := Add (S, K);
pragma Loop_Invariant (Integer (Length (S)) = K);
pragma Loop_Invariant
(for all J in 1 .. K => Get (S, J) = J);
end loop;
return S;
end Create;
begin
null;
end Example_10;
This code is correct.